Fit head-direction population

Fit head-direction population#

This notebook has had all its explanatory text removed and has not been run. It is intended to be downloaded and run locally (or on the provided binder) while listening to the presenter’s explanation. In order to see the fully rendered of this notebook, go here

Learning objectives#

Include history-related predictors to NeMoS GLM.
Reduce over-fitting with Basis.
Learn functional connectivity.

import matplotlib.pyplot as plt
import numpy as np
import pynapple as nap

import nemos as nmo

# some helper plotting functions
from nemos import _documentation_utils as doc_plots
import workshop_utils

# configure pynapple to ignore conversion warning
nap.nap_config.suppress_conversion_warnings = True

# configure plots some
plt.style.use(nmo.styles.plot_style)

Data Streaming#

Fetch the data.

path = workshop_utils.fetch.fetch_data("Mouse32-140822.nwb")

Pynapple#

load_file : open the NWB file and give a preview.

data = nap.load_file(path)

data

Load the units

spikes = data["units"]

spikes

Load the epochs and take only wakefulness

epochs = data["epochs"]
wake_epochs = epochs[epochs.tags == "wake"]

Load the angular head-direction of the animal (in radians)

angle = data["ry"]

Select only those units that are in ADn
Restrict the activity to wakefulness (both the spiking activity and the angle)

spikes = spikes[spikes.location == "adn"]

spikes = spikes.restrict(wake_epochs).getby_threshold("rate", 1.0)
angle = angle.restrict(wake_epochs)

Compute tuning curves as a function of head-direction

tuning_curves = nap.compute_1d_tuning_curves(
    group=spikes, feature=angle, nb_bins=61, minmax=(0, 2 * np.pi)
)

Plot the tuning curves.

fig, ax = plt.subplots(1, 2, figsize=(12, 4))
ax[0].plot(tuning_curves.iloc[:, 0])
ax[0].set_xlabel("Angle (rad)")
ax[0].set_ylabel("Firing rate (Hz)")
ax[1].plot(tuning_curves.iloc[:, 1])
ax[1].set_xlabel("Angle (rad)")
plt.tight_layout()

Let’s visualize the data at the population level.

fig = workshop_utils.plot_head_direction_tuning_model(
    tuning_curves, spikes, angle, threshold_hz=1, start=8910, end=8960
)

Define a wake_ep IntervalSet with the first 3 minutes of wakefulness (to speed up model fitting).

wake_ep =

bin the spike trains in 10 ms bin (count = ...).

bin_size =
count =

sort the neurons by their preferred direction using pandas:
- Preferred angle: pref_ang = tuning_curves.idxmax().
- Define a new count TsdFrame, sorting the columns according to pref_ang.

pref_ang = tuning_curves.idxmax()
# sort the columns by angle
count = nap.TsdFrame(

NeMoS#

Self-Connected Single Neuron#

Start with modeling a self-connected single neuron.
Select a neuron (call the variable neuron_count).
Select the first 1.2 seconds for visualization. (call the epoch epoch_one_spk).

# select neuron 0 spike count time series
neuron_count =
# restrict to a smaller time interval (1.2 sec)
epoch_one_spk =

Features Construction#

Fix a history window of 800ms (0.8 seconds).
Plot the result using doc_plots.plot_history_window

# set the size of the spike history window in seconds
window_size_sec = 0.8

doc_plots.plot_history_window(neuron_count, epoch_one_spk, window_size_sec);

By shifting the time window we can predict new count bins.
Concatenating all the shifts, we form our feature matrix.

doc_plots.run_animation(neuron_count, epoch_one_spk.start[0])

This is equivalent to convolving count with an identity matrix.
That’s what NeMoS HistoryConv basis is for:
- Convert the window size in number of bins (call it window_size)
- Define an HistoryConv basis covering this window size (call it history_basis).
- Create the feature matrix with history_basis.compute_features (call it input_feature).

# convert the prediction window to bins (by multiplying with the sampling rate)
window_size =
# define the history bases
history_basis =
# create the feature matrix
input_feature =

NeMoS NaN pads if there aren’t enough samples to predict the counts.

# print the NaN indices along the time axis
print("NaN indices:\n", np.where(np.isnan(input_feature[:, 0]))[0]) 

Check the shape of the counts and features.

# enter code here

Plot the convolution output with workshop_utils.plot_features.

suptitle = "Input feature: Count History"
neuron_id = 0
workshop_utils.plot_features(input_feature, count.rate, suptitle);

Fitting the Model#

Split your epochs in two for validation purposes:
- Define two IntervalSets, each with half of the input_feature.time_support duration

# construct the train and test epochs
duration = input_feature.time_support.tot_length("s")
start = input_feature.time_support["start"]
end = input_feature.time_support["end"]

# define the interval sets
first_half = nap.IntervalSet(start, start + duration / 2)
second_half = nap.IntervalSet(start + duration / 2, end)

Fit a GLM to the first half.

# define the GLM object
model = 
# Fit over the training epochs

Plot the weights (model.coef_).

plt.figure()
plt.title("Spike History Weights")
plt.plot(np.arange(window_size) / count.rate, np.squeeze(model.coef_), lw=2, label="GLM raw history 1st Half")
plt.axhline(0, color="k", lw=0.5)
plt.xlabel("Time From Spike (sec)")
plt.ylabel("Kernel")
plt.legend()

Inspecting the results#

Fit on the other half.

# fit on the test set
model_second_half = 

Compare results.

plt.figure()
plt.title("Spike History Weights")
plt.plot(np.arange(window_size) / count.rate, np.squeeze(model.coef_),
         label="GLM raw history 1st Half", lw=2)
plt.plot(np.arange(window_size) / count.rate,  np.squeeze(model_second_half.coef_),
         color="orange", label="GLM raw history 2nd Half", lw=2)
plt.axhline(0, color="k", lw=0.5)
plt.xlabel("Time From Spike (sec)")
plt.ylabel("Kernel")
plt.legend()

Reducing feature dimensionality#

Visualize the raised cosine basis.

doc_plots.plot_basis();

Define the basis RaisedCosineLogConvand name it basis.
Basis parameters:
- 8 basis functions.
- Window size of 0.8sec.

# a basis object can be instantiated in "conv" mode for convolving  the input.
basis =

Convolve the counts with the basis functions. (Call the output conv_spk)
Print the shape of conv_spk and compare it to input_feature.

# convolve the basis
conv_spk =
# print the shape
print(f"Raw count history as feature: {input_feature.shape}")
print(f"Compressed count history as feature: {conv_spk.shape}")

Visualize the output.

# Visualize the convolution results
epoch_one_spk = nap.IntervalSet(8917.5, 8918.5)
epoch_multi_spk = nap.IntervalSet(8979.2, 8980.2)

doc_plots.plot_convolved_counts(neuron_count, conv_spk, epoch_one_spk, epoch_multi_spk);

Fit and compare the models#

Fit the model using the compressed features. Call it model_basis.

# use restrict on interval set training and fit a GLM
model_basis =

Reconstruct the history filter:
- Extract the basis kernels with _, basis_kernels = basis.evaluate_on_grid(window_size).
- Multiply the basis_kernel with the coefficient using np.matmul.
Check the shape of self_connection.

# get the basis function kernels
_, basis_kernels = 
# multiply with the weights
self_connection = 
# print the shape of self_connection

Check if with less parameter we are not over-fitting.
Fit the other half of the data. Name it model_basis_second_half.

model_basis_second_half =

Get the response filters: multiply the basis_kernels with the weights from model_basis_second_half.
Call the output self_connection_second_half.

self_connection_second_half =

Plot and compare the results.

time = np.arange(window_size) / count.rate
plt.figure()
plt.title("Spike History Weights")
plt.plot(time, np.squeeze(model.coef_), "k", alpha=0.3, label="GLM raw history 1st half")
plt.plot(time, np.squeeze(model_second_half.coef_), alpha=0.3, color="orange", label="GLM raw history 2nd half")
plt.plot(time, self_connection, "--k", lw=2, label="GLM basis 1st half")
plt.plot(time, self_connection_second_half, color="orange", lw=2, ls="--", label="GLM basis 2nd half")
plt.axhline(0, color="k", lw=0.5)
plt.xlabel("Time from spike (sec)")
plt.ylabel("Weight")
plt.legend()

Predict the rates from model and model_basis. Call it rate_history and rate_basis.
Convert the rate from spike/bin to spike/sec by multiplying with conv_spk.rate.

# enter code here

Plot the results.

ep = nap.IntervalSet(start=8819.4, end=8821)
# plot the rates
doc_plots.plot_rates_and_smoothed_counts(
    neuron_count,
    {"Self-connection raw history":rate_history, "Self-connection bsais": rate_basis}
);

All-to-all Connectivity#

Preparing the features#

Re-define the basis.
Convolve all counts. Call the output in convolved_count.
Print the output shape

# reset the input shape by passing the pop. count
basis =
# convolve all the neurons
convolved_count = 

Fitting the Model#

Fit a PopulationGLM, call the object model
Use Ridge regularization with a regularizer_strength=0.1
Print the shape of the estimated coefficients.

model =
print(f"Model coefficients shape: {model.coef_.shape}")

Comparing model predictions.#

Predict the firing rate of each neuron. Call it predicted_firing_rate.
Convert the rate from spike/bin to spike/sec.

predicted_firing_rate =

Visualize the predicted rate and tuning function.

# use pynapple for time axis for all variables plotted for tick labels in imshow
workshop_utils.plot_head_direction_tuning_model(tuning_curves, spikes, angle, 
                                                predicted_firing_rate, threshold_hz=1,
                                                start=8910, end=8960, cmap_label="hsv");

Visually compare all the models.

fig = doc_plots.plot_rates_and_smoothed_counts(
    neuron_count,
    {"Self-connection: raw history": rate_history,
     "Self-connection: bsais": rate_basis,
     "All-to-all: basis": predicted_firing_rate[:, 0]}
)

Visualizing the connectivity#

Check the shape of the weights.

# enter code here

Reshape the weights with basis.split_by_feature (returns a dictionary).

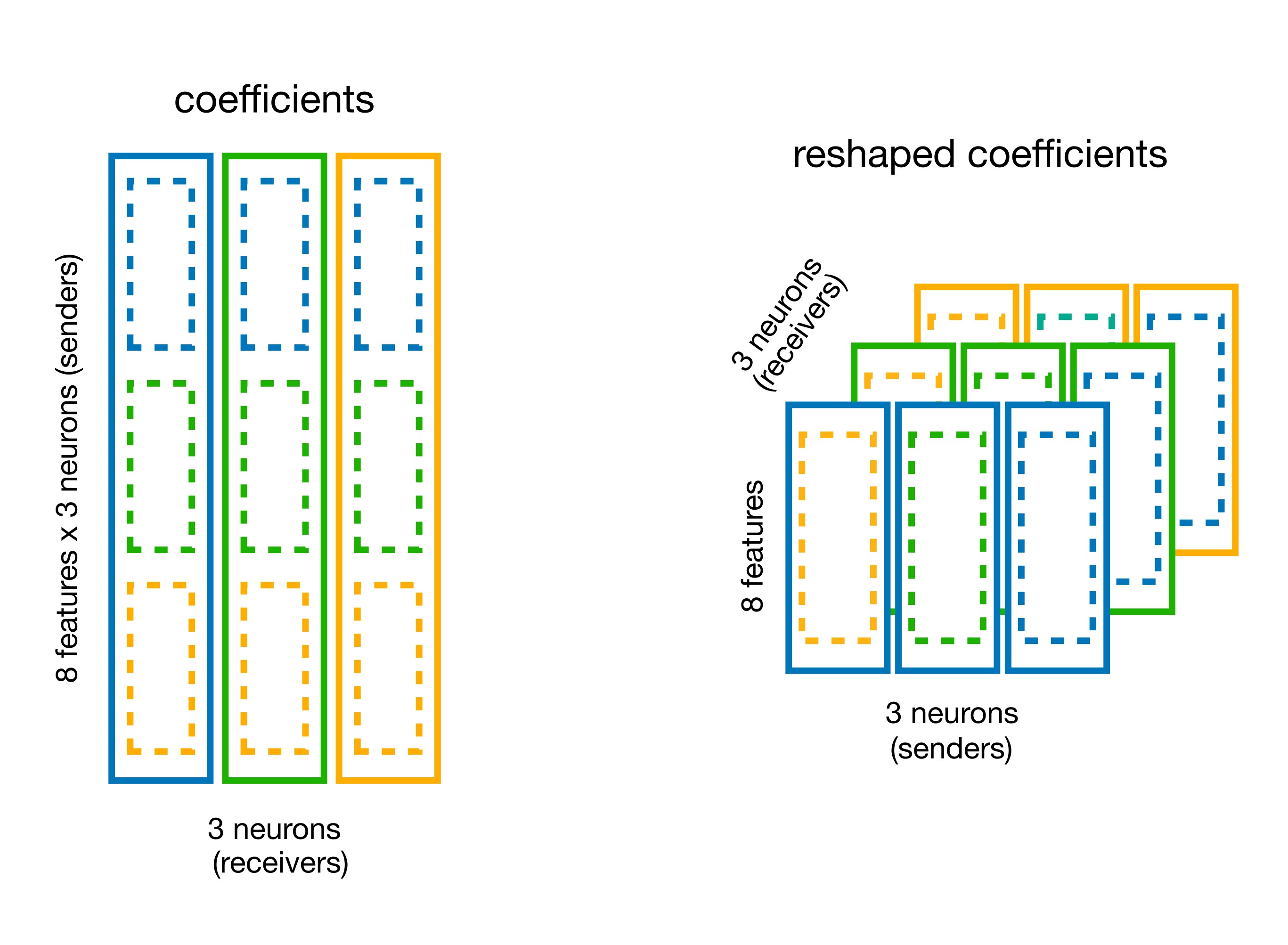
Reshape coefficients

# split the coefficient vector along the feature axis (axis=0)
weights_dict =
# visualize the content
weights_dict

Get the weight array from the dictionary (and call the output weights).
Print the new shape of the weights.

# get the coefficients
weights = 
# print the shape
print(

The shape is (sender_neuron, num_basis, receiver_neuron).
Multiply the weights with the kernels with: np.einsum("jki,tk->ijt", weights, basis_kernels).
Call the output responses and print its shape.

responses = np.einsum("jki,tk->ijt", weights, basis_kernels)

print(responses.shape)

Plot the connectivity map.

tuning = nap.compute_1d_tuning_curves_continuous(predicted_firing_rate,
                                                 feature=angle,
                                                 nb_bins=61,
                                                 minmax=(0, 2 * np.pi))
                                                 
fig = doc_plots.plot_coupling(responses, tuning)

Fit head-direction population

Contents

Fit head-direction population#

Learning objectives#

Data Streaming#

Pynapple#

NeMoS#

Self-Connected Single Neuron#

Features Construction#

Fitting the Model#

Inspecting the results#

Reducing feature dimensionality#

Fit and compare the models#

All-to-all Connectivity#

Preparing the features#

Fitting the Model#

Comparing model predictions.#

Visualizing the connectivity#