Download
This notebook can be downloaded as visual_coding.ipynb. See the button at the top right to download as markdown or pdf.
Exploring the Visual Coding Dataset#
This notebook serves as a group project: in groups of 4 or 5, you will analyze data from the Visual Coding - Neuropixels dataset, published by the Allen Institute. This dataset uses extracellular electrophysiology probes to record spikes from multiple regions in the brain during passive visual stimulation.
To start, we will focus on the activity of neurons in the visual cortex (VISp) during passive exposure to full-field flashes of color either black (coded as “-1.0”) or white (coded as “1.0”) in a gray background. If you have time, you can apply the same procedure to other stimuli or brain areas.
For this exercise, you will:
Compute Peristimulus Time Histograms (PSTHs) and select relevant neurons to analyze using
pynapple.Fit GLMs to these neurons using
nemos.
As this is the last notebook, the instructions are a bit more hands-off: you will make more of the analysis and modeling decisions yourselves. As a group, you will use your neuroscience knowledge and the skills gained over this workshop to decide:
How to select relevant neurons.
How to avoid overfitting.
What features to include in your GLMs.
Which basis functions (and parameters) to use for each feature.
How to regularize your features.
How to evaluate your model.
At the end of this session, we will regroup to discuss the decisions people made and evaluate each others’ models.
This notebook is adapted from Camila Maura’s Intro to GLM notebook in the Allen Institute OpenScope Databook. See that notebook for a thorough introduction to using pynapple and nemos by fitting this dataset.
# Import everything
import jax
import matplotlib.pyplot as plt
import numpy as np
import pynapple as nap
import nemos as nmo
# some helper plotting functions
from nemos import _documentation_utils as doc_plots
import workshop_utils
import matplotlib as mpl
from matplotlib.ticker import MaxNLocator
from scipy.stats import gaussian_kde
from matplotlib.patches import Patch
# configure plots some
plt.style.use(nmo.styles.plot_style)
WARNING:2025-10-24 20:36:27,073:jax._src.xla_bridge:850: An NVIDIA GPU may be present on this machine, but a CUDA-enabled jaxlib is not installed. Falling back to cpu.
Downloading and preparing data#
First we download and load the data into pynapple.
# Dataset information
dandiset_id = "000021"
dandi_filepath = "sub-726298249/sub-726298249_ses-754829445.nwb"
# Download the data using NeMoS
io = nmo.fetch.download_dandi_data(dandiset_id, dandi_filepath)
# load data using pynapple
data = nap.NWBFile(io.read(), lazy_loading=True)
# grab the spiking data
units = data["units"]
# map from electrodes to brain area
channel_probes = {}
for elec in data.nwb.electrodes:
channel_id = elec.index[0]
location = elec["location"].values[0]
channel_probes[channel_id] = location
# Add a new column to include location in our spikes TsGroup
units.brain_area = [channel_probes[int(ch_id)] for ch_id in units.peak_channel_id]
# drop unnecessary metadata
units.restrict_info(["rate", "quality", "brain_area"])
Now that we have our spiking data, let’s restrict our dataset to the relevant part.
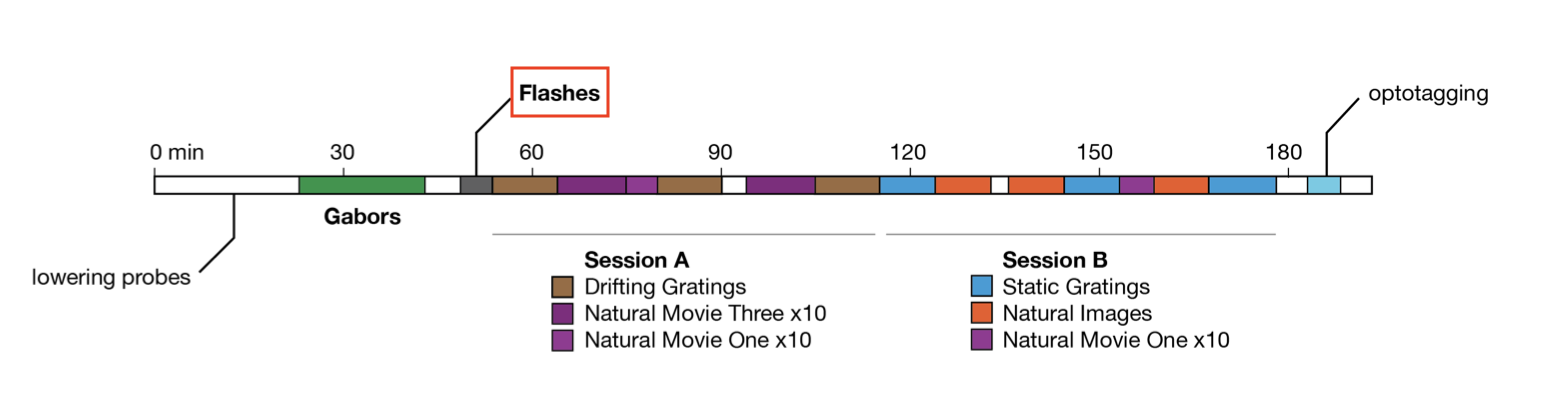
During the flashes presentation trials, mice were exposed to white or black full-field flashes in a gray background, each lasting 250 ms, and separated by a 2 second inter-trial interval. In total, they were exposed to 150 flashes (75 black, 75 white).
flashes = data["flashes_presentations"]
flashes.restrict_info(["color"])
# create a separate object for black and white flashes
flashes_white = flashes[flashes["color"] == "1.0"]
flashes_black = flashes[flashes["color"] == "-1.0"]
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/metadata_class.py:167: UserWarning: Metadata name 'size' overlaps with an existing attribute, and cannot be accessed as an attribute or key. Use 'get_info()' to access metadata.
warnings.warn(
Other stimulus classes?
As can be seen in the image above, there are many other stimulus types shown in this experiment. If you finish analyzing the flashes and want to look at one of the others, you can do so by grabbing the corresponding IntervalSet from the data object; they are all named {stim_type}_presentations, where {stim_type} may be flashes, gabors, static_gratings, etc.
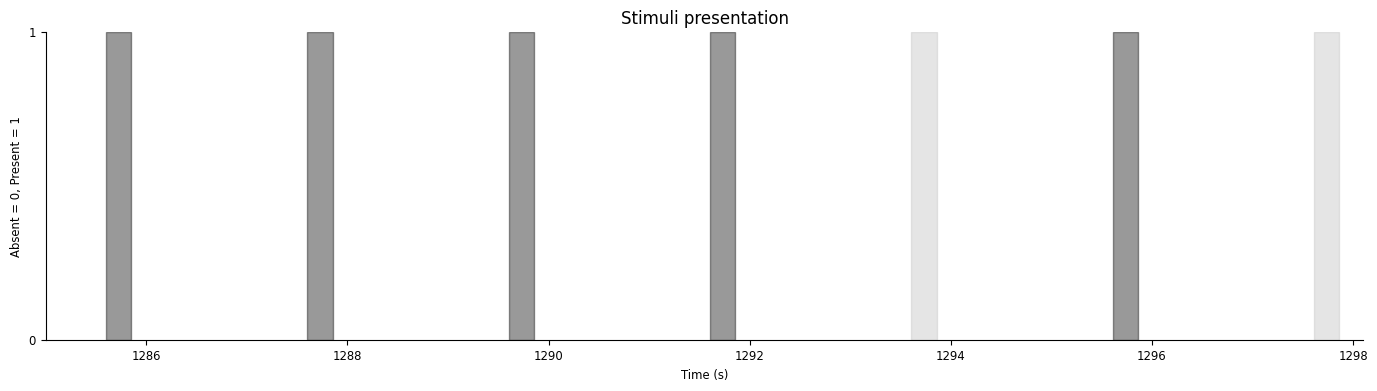
Let’s visualize our stimuli:
(1285.000869922, 1298.100869922)
Preliminary analyses and neuron selection#
From here on out, you will write the code yourself. This first section will involve us doing some preliminary analyses to find the neurons that are most visually responsive; these are the neurons we will fit our GLM to.
First, let’s construct a IntervalSet called extended_flashes which contains the peristimulus time. Right now, our flashes IntervalSet defines the start and end time for the flashes. In order to make sure we can model the pre-stimulus baseline and any responses to the stimulus being turned off, we would like to expand these intervals to go from 500 msecs before the start of the stimuli to 500 msecs after the end.
This IntervalSet should be the same shape as flashes and have the same metadata columns.
dt = .50 # 500 ms
start = flashes.start - dt # Start 500 ms before stimulus presentation
end = flashes.end + dt # End 500 ms after stimulus presentation
extended_flashes = nap.IntervalSet(start, end, metadata=flashes.metadata)
If you have succeeded, the following should pass:
assert extended_flashes.shape == flashes.shape
assert all(extended_flashes.metadata == flashes.metadata)
assert all(extended_flashes.start == flashes.start - .5)
assert all(extended_flashes.end == flashes.end + .5)
Now, create two separate IntervalSet objects, extended_flashes_black and extended_flashes_white, which contain this info for only the black and the white flashes, respectively.
extended_flashes_white = extended_flashes[extended_flashes["color"] == "1.0"]
extended_flashes_black = extended_flashes[extended_flashes["color"] == "-1.0"]
# OR
dt = .50 # 500 ms
start = flashes_white.start - dt # Start 500 ms before stimulus presentation
end = flashes_white.end + dt # End 500 ms after stimulus presentation
extended_flashes_white = nap.IntervalSet(start, end, metadata=flashes_white.metadata)
start = flashes_black.start - dt # Start 500 ms before stimulus presentation
end = flashes_black.end + dt # End 500 ms after stimulus presentation
extended_flashes_black = nap.IntervalSet(start, end, metadata=flashes_black.metadata)
# This should all pass if you created the IntervalSet correctly
assert extended_flashes_white.shape == flashes_white.shape
assert all(extended_flashes_white.metadata == flashes_white.metadata)
assert all(extended_flashes_white.start == flashes_white.start - .5)
assert all(extended_flashes_white.end == flashes_white.end + .5)
assert extended_flashes_black.shape == flashes_black.shape
assert all(extended_flashes_black.metadata == flashes_black.metadata)
assert all(extended_flashes_black.start == flashes_black.start - .5)
assert all(extended_flashes_black.end == flashes_black.end + .5)
Now, select your neurons. There are four criteria we want to use:
Brain area: we are interested in analyzing VISp units for this tutorial
Quality: we will only select “good” quality units. If you’re curious, you can (optionally) read more how about the Allen Institute defines quality.
Firing rate: overall, we want units with a firing rate larger than 2Hz around the presentation of stimuli
Responsiveness: we want units that actually respond to changes in the visual stimuli, i.e., their firing rate changes as a result of the stimulus.
Create a new TsGroup, selected_units, which includes only those units that meet the first three criteria, then check that it passes the assertion block.
Restrict!
Don’t forget when selecting based on firing rate that we want neurons whose firing rate is above the threshold around the presentation of the stimuli! This means you should use restrict()! If only we had a useful IntervalSet lying around…
# Filter units according criteria 1 & 2
selected_units = units[(units["brain_area"]=="VISp") & (units["quality"]=="good")]
# Restrict around stimuli presentation
selected_units = selected_units.restrict(extended_flashes)
# Filter according to criterion 3
selected_units = selected_units[(selected_units["rate"]>2.0)]
assert len(selected_units) == 92
Now, in order to determine the responsiveness of the units, it’s helpful to use the compute_perievent() function: this will align units’ spiking timestamps with the onset of the stimulus repetitions and take an average over them.
Let’s use that function to construct two separate perievent dictionaries, one aligned to the start of the white stimuli, one aligned to the start of the black, and they should run from 250 msec before to 500 msec after the event.
# Set window of perievent 500 ms before and after the start of the event
window_size = (-.250, .500)
# Re-center timestamps for white stimuli
# +50 because we subtracted 500 ms at beginning of stimulus presentation
peri_white = nap.compute_perievent(timestamps=selected_units,
tref=nap.Ts(extended_flashes_white.start +.50),
minmax=window_size)
# Re-center timestamps for black stimuli
# +50 because we subtracted 500 ms at beginning of stimulus presentation
peri_black = nap.compute_perievent(timestamps=selected_units,
tref=nap.Ts(extended_flashes_black.start +.50),
minmax=window_size)
# OR
peri_white = nap.compute_perievent(timestamps=selected_units,
tref=nap.Ts(flashes_white.start),
minmax=window_size)
peri_black = nap.compute_perievent(timestamps=selected_units,
tref=nap.Ts(flashes_black.start),
minmax=window_size)
assert len(peri_white) == len(selected_units)
assert ([p.ref_times for p in peri_white.values()] == flashes_white.start).all()
assert len(peri_black) == len(selected_units)
assert ([p.ref_times for p in peri_black.values()] == flashes_black.start).all()
Visualizing these perievents can help us determine which units to include. The following helper function should help.
# called like this, the function will visualize the first 9 units. play with the n_units
# and start_unit arguments to see the other units.
plot_raster_psth(peri_white, selected_units, "white", n_units=9, start_unit=0)
plot_raster_psth(peri_black, selected_units, "black", n_units=9, start_unit=0)

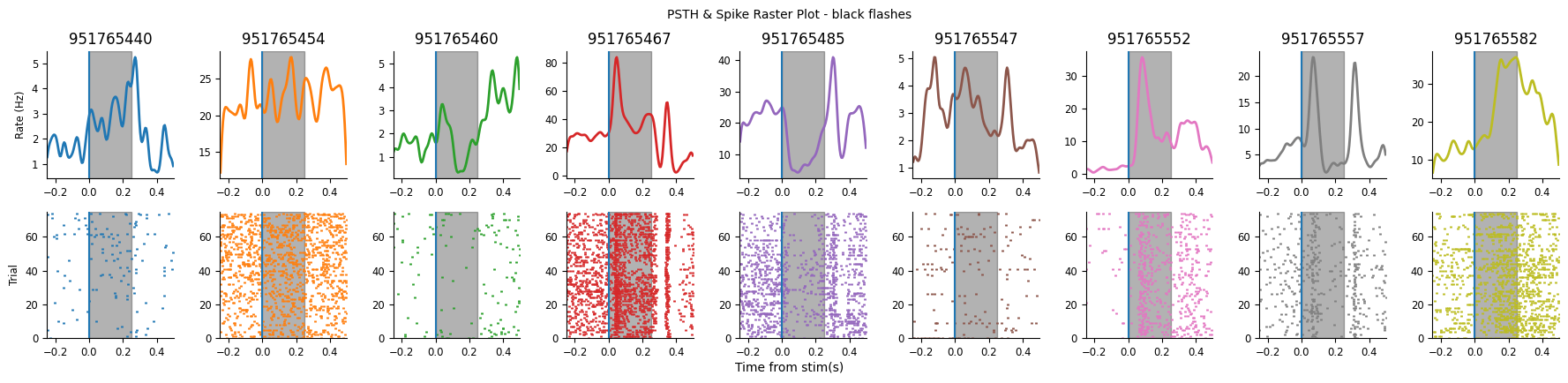
You could manually visualize each of our units and select those that appear, from their PSTH to be responsive.
However, it would be easier to scale (and more reproducible) if you came up with some measure of responsiveness. So how do we compute something that captures “this neuron responds to visual stimuli”?
You should be able to do this using a function that iterates over the peri_white and peri_black dictionaries, returning a single float for each unit.
Let’s aim to pick around 20 neurons.
If you’re having trouble coming up with one that seems reasonable, expand the following admonition.
How to compute responsiveness?
Try defining responsiveness as the normalized difference in average firing rate between during stimulus presentation and before the stimulus was presented.
We can use restrict() together with np.mean to compute the average firing rates above, and then combine them.
From here on out, I predict that the participant notebooks are going to start diverging pretty drastically. So we’ll show one possibility, but other solutions, as long as they’re reasonable, are fine.
For responsiveness, we’ll define it as the normalized difference between during stimulus and pre-stimulus average firing rate.
def get_responsiveness(perievents, bin_size=0.005):
"""Calculate responsiveness for each neuron. This is computed as:
post_presentation_avg :
Average firing rate during presentation (250 ms) of stimulus across
all instances of stimulus.
pre_presentation_avg :
Average firing rate prior (250 ms) to the presentation of stimulus
across all instances prior of stimulus.
responsiveness :
abs((post_presentation_avg - pre_presentation_avg) / (post_presentation_avg + pre_presentation_avg))
Larger values indicate higher responsiveness to the stimuli.
Parameters
----------
perievents : TsGroup
Contains perievent information of a subset of neurons
bin_size : float
Bin size for calculating spike counts
Returns
----------
resp_array : np.array
Array of responsiveness information.
"""
resp_dict = {}
resp_array = np.zeros(len(perievents.keys()), dtype=float)
for index, peri in enumerate(perievents.values()):
# Count the number of timestamps in each bin_size bin.
peri_counts = peri.count(bin_size)
# Compute average spikes for each millisecond in the
# the 250 ms before stimulus presentation
pre_presentation = np.mean(peri_counts, 1).restrict(nap.IntervalSet([-.25,0]))
# Compute average spikes for each millisecond in the
# the 250 ms after stimulus presentation
post_presentation = np.mean(peri_counts, 1).restrict(nap.IntervalSet([0,.25]))
pre_presentation_avg = np.mean(pre_presentation)
post_presentation_avg = np.mean(post_presentation)
responsiveness = abs((post_presentation_avg - pre_presentation_avg) / (post_presentation_avg + pre_presentation_avg))
resp_array[index] = responsiveness
return resp_array
responsiveness_white = get_responsiveness(peri_white)
responsiveness_black = get_responsiveness(peri_black)
# Get threshold for top 15% most responsive
thresh_black = np.percentile(responsiveness_black, 85)
thresh_white = np.percentile(responsiveness_white, 85)
# Only keep units that are within the 15% most responsive for either black or white
selected_units = selected_units[(responsiveness_black > thresh_black) | (responsiveness_white > thresh_white)]
Let’s visualize the selected units PSTHs to make sure they all look reasonable:
print(f"Remaining units: {len(selected_units)}")
peri_white = {k: peri_white[k] for k in selected_units.index}
peri_black = {k: peri_black[k] for k in selected_units.index}
plot_raster_psth(peri_black, selected_units, "black", n_units=len(peri_black))
plot_raster_psth(peri_white, selected_units, "white", n_units=len(peri_white))
Remaining units: 19


Avoiding overfitting#
As we’ve seen throughout this workshop, it is important to avoid overfitting your model. We’ve covered two strategies for doing so: either separate your dataset into train and test subsets or set up a cross-validation scheme. Pick one of these approaches and use it when fitting your GLM model in the next section.
You might find it helpful to refer back to the sklearn notebook and / or to use the following pynapple functions: set_diff(), union(), restrict().
Again, multiple viable ways of solving this. Here’s the simplest: grab every third flash and use that as the test set.
# We take one every three flashes (33% of all flashes of test)
flashes_test_white = extended_flashes_white[::3]
flashes_test_black = extended_flashes_black[::3]
# The remaining is separated for training
flashes_train_white = extended_flashes_white.set_diff(flashes_test_white)
flashes_train_black = extended_flashes_black.set_diff(flashes_test_black)
# Merge both stimuli types in a single interval set
flashes_test = flashes_test_white.union(flashes_test_black)
flashes_train = flashes_train_white.union(flashes_train_black)
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/interval_set.py:708: UserWarning: metadata incompatible with union method. dropping metadata from result
warnings.warn(
Fit a GLM#
In this section, you will use nemos to build a GLM. There are a lot of scientific decisions to be made here, so we suggest starting simple and then adding complexity. Construct a design matrix with a single predictor, using a basis of your choice, then construct, fit, and score your model to a single neuron (remembering to either use your train/test or cross-validation to avoid overfitting). Then add regularization to your GLM. Then return to the beginning and add more predictors. Then fit all the neurons. Then evaluate what basis functions and parameters are best for your predictors. Then use the tricks we covered in sklearn to evaluate whether which predictors are necessary for your model, which are the most important.
You don’t have to exactly follow those steps, but make sure you can go from beginning to end before getting too complex.
Good luck and we look forward to seeing what you come up with!
There are many ways to do this. We’ll show fitting a single neuron GLM to a variety of stimulus-derived predictors. You can also see the original notebook for a PopulationGLM that adds coupling.
Prepare data#
Create spike count data.
# General spike counts
bin_size = .005
units_counts = selected_units.count(bin_size, ep=extended_flashes)
Construct design matrix#
Decide on feature(s)
Decide on basis
Construct design matrix
What features should I include?
If you’re having trouble coming up with features to include, here are some possibilities:
Stimulus.
Stimulus onset.
Stimulus offset.
For multiple neurons: neuron-to-neuron coupling.
For the stimuli predictors, you probably want to model white and black separately.
Here we’ll model three separate components of the response:
Flash onset (beginning): We will convolve the early phase of the flash presentation with a basis function. This allows for fine temporal resolution immediately after stimulus onset, where rapid neural responses are often expected.
Flash offset (end): We will convolve the later phase of the flash (around its end) with a different basis function. This emphasizes activity changes around stimulus termination.
Full flash duration (smoothing): We will convolve the entire flash period with a third basis function, serving as a smoother to capture more sustained or slowly varying effects across the full stimulus window.
# Create a TsdFrame filled by zeros, for the size of units_counts
stim = nap.TsdFrame(
t=units_counts.t,
d=np.zeros((len(units_counts), 2)),
columns = ['white', 'black']
)
# Check whether there is a flash within a given bin of spikes
# If there is not, put a nan in that index
idx_white = flashes_white.in_interval(units_counts)
idx_black = flashes_black.in_interval(units_counts)
# Replace everything that is not nan with 1 in the corresponding column
stim.d[~np.isnan(idx_white), 0] = 1
stim.d[~np.isnan(idx_black), 1] = 1
white_onset = nap.Tsd(
t=stim.t,
d=np.hstack((0,np.diff(stim["white"])==1)),
time_support = units_counts.time_support
)
white_offset = nap.Tsd(
t=stim.t,
d=np.hstack((0,np.diff(stim["white"])==-1)),
time_support = units_counts.time_support
)
black_onset = nap.Tsd(
t=stim.t,
d=np.hstack((0,np.diff(stim["black"])==1)),
time_support = units_counts.time_support
)
black_offset = nap.Tsd(
t=stim.t,
d=np.hstack((0,np.diff(stim["black"])==-1)),
time_support = units_counts.time_support
)
Now set up the basis functions
# Duration of stimuli
stimulus_history_duration = 0.250
# Window length in bin size units
window_len = int(stimulus_history_duration / bin_size)
# Initialize basis objects
basis_white_on = nmo.basis.RaisedCosineLogConv(
n_basis_funcs=5,
window_size=window_len,
label="white_on"
)
basis_white_off = nmo.basis.RaisedCosineLinearConv(
n_basis_funcs=5,
window_size=window_len,
label="white_off",
conv_kwargs={"predictor_causality":"acausal"}
)
basis_white_stim= nmo.basis.RaisedCosineLogConv(
n_basis_funcs=5,
window_size=window_len,
label="white_stim"
)
basis_black_on = nmo.basis.RaisedCosineLogConv(
n_basis_funcs=5,
window_size=window_len,
label="black_on"
)
basis_black_off = nmo.basis.RaisedCosineLinearConv(
n_basis_funcs=5,
window_size=window_len,
label="black_off",
conv_kwargs={"predictor_causality":"acausal"}
)
basis_black_stim = nmo.basis.RaisedCosineLogConv(
n_basis_funcs=5,
window_size=window_len,
label="black_stim"
)
# Define additive basis object to construct design matrix
additive_basis = (
basis_white_on +
basis_white_off +
basis_white_stim +
basis_black_on +
basis_black_off +
basis_black_stim
)
Construct design matrix, separately for test and train.
# Convolve basis with inputs - test set
X_test = additive_basis.compute_features(
white_onset.restrict(flashes_test),
white_offset.restrict(flashes_test),
stim["white"].restrict(flashes_test),
black_onset.restrict(flashes_test),
black_offset.restrict(flashes_test),
stim["black"].restrict(flashes_test)
)
# Convolve basis with inputs - train set
X_train = additive_basis.compute_features(
white_onset.restrict(flashes_train),
white_offset.restrict(flashes_train),
stim["white"].restrict(flashes_train),
black_onset.restrict(flashes_train),
black_offset.restrict(flashes_train),
stim["black"].restrict(flashes_train)
)
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/nemos/convolve.py:416: UserWarning: With `acausal` filter, `basis_matrix.shape[0] should probably be odd, so that we can place an equal number of NaNs on either side of input.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/nemos/convolve.py:416: UserWarning: With `acausal` filter, `basis_matrix.shape[0] should probably be odd, so that we can place an equal number of NaNs on either side of input.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/nemos/convolve.py:416: UserWarning: With `acausal` filter, `basis_matrix.shape[0] should probably be odd, so that we can place an equal number of NaNs on either side of input.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/nemos/convolve.py:416: UserWarning: With `acausal` filter, `basis_matrix.shape[0] should probably be odd, so that we can place an equal number of NaNs on either side of input.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
/home/agent/workspace/rorse_ccn-software-sfn-2025_main/lib/python3.12/site-packages/pynapple/core/utils.py:196: UserWarning: Converting 'd' to numpy.array. The provided array was of type 'ArrayImpl'.
warnings.warn(
Construct and fit your model#
Decide on regularization
Initialize GLM
Call fit
Visualize result on PSTHs
Here’s an example of how this could look for a single neuron. To do multiple neurons, model should be a PopulationGLM and fit to units_counts.restrict(flashes_train) instead.
(The following regularizer strength comes from cross-validation.)
regularizer_strength = 7.745e-06
# Initialize model object of a single unit
model = nmo.glm.GLM(
regularizer="Ridge",
regularizer_strength=regularizer_strength,
solver_name="LBFGS",
)
# Choose an example unit
unit_id = 951768318
# Get counts for train and test for said unit
u_counts = units_counts.loc[unit_id]
model.fit(X_train, u_counts.restrict(flashes_train))
GLM(
observation_model=PoissonObservations(),
inverse_link_function=exp,
regularizer=Ridge(),
regularizer_strength=7.745e-06,
solver_name='LBFGS'
)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| observation_model | PoissonObservations() | |
| inverse_link_function | <PjitFunction...7f07e980e8e0>> | |
| regularizer | Ridge() | |
| regularizer_strength | 7.745e-06 | |
| solver_name | 'LBFGS' | |
| solver_kwargs | {} |
# Use predict to obtain the firing rates
pred_unit = model.predict(X_test)
# Convert units from spikes/bin to spikes/sec
pred_unit = pred_unit/ bin_size
# Re-center timestamps around white stimuli
# +50 because we subtracted .50 at beginning of stimulus presentation
peri_white_pred_unit = nap.compute_perievent_continuous(
timeseries=pred_unit,
tref=nap.Ts(flashes_test_white.start+.50),
minmax=window_size
)
# Re-center timestamps for black stimuli
# +50 because we subtracted .50 at beginning of stimulus presentation
peri_black_pred_unit = nap.compute_perievent_continuous(
timeseries=pred_unit,
tref=nap.Ts(flashes_test_black.start+.50),
minmax=window_size
)
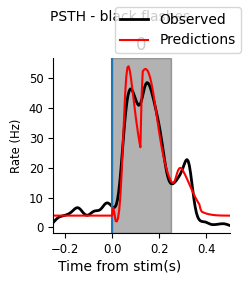
Here’s a helper function for plotting the PSTH of the data and predictions (for one or multiple neurons), which you may find helpful for visualizing your model performance.
plot_pop_psth(peri_white[unit_id], "white", predictions=("red", peri_white_pred_unit))
plot_pop_psth(peri_black[unit_id], "black", predictions=("red", peri_black_pred_unit))

Score your model#
We trained on the train set, so now we score on the test set. (Or use cross-validation.)
Get a score for your model that you can use to compare across the modeling choices outlined above.
# Calculate the mean score for the Stimuli + Coupling model
# using pseudo-r2-McFadden
score = model.score(
X_test,
u_counts.restrict(flashes_test),
score_type="pseudo-r2-McFadden"
)
print(score)
0.141631
Try to improve your model?#
Go back to the beginning of this section and try to improve your model’s performance (as reflected by increased score).
Keep track of what you’ve tried and their respective scores.
You can do this by hand, but constructing a pandas DataFrame, as we’ve seen in
sklearn, is useful:
# Example construction of dataframe.
# In this:
# - additive_basis is the single AdditiveBasis object we used to construct the entire design matrix
# - model is the GLM we fit to a single neuron
# - unit_id is the int identifying the neuron we're fitting
# - score is the float giving the model score, summarizing model performance (on the test set)
import pandas as pd
data = [
{
"model_id": 0,
"regularizer": model.regularizer.__class__.__name__,
"regularizer_strength": model.regularizer_strength,
"solver": model.solver_name,
"score": score,
"n_predictors": len(additive_basis),
"unit": unit_id,
"predictor_i": i,
"predictor": basis.label.strip(),
"basis": basis.__class__.__name__,
# any other info you think is important ...
}
for i, basis in enumerate(additive_basis)
]
df = pd.DataFrame(data)
df
| model_id | regularizer | regularizer_strength | solver | score | n_predictors | unit | predictor_i | predictor | basis | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 0 | white_on | RaisedCosineLogConv |
| 1 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 1 | white_off | RaisedCosineLinearConv |
| 2 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 2 | white_stim | RaisedCosineLogConv |
| 3 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 3 | black_on | RaisedCosineLogConv |
| 4 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 4 | black_off | RaisedCosineLinearConv |
| 5 | 0 | Ridge | 0.000008 | LBFGS | 0.141631 | 6 | 951768318 | 5 | black_stim | RaisedCosineLogConv |
