Examples

This page gives one step-by-step example of the most basic usage of the DLR within cppdlr. For a basic overview of the DLR, definitions, and conventions, please see the background page.

Further examples, containing thorough documentation of all steps, can be found in the examples directory of the repository. The list of examples below gives a list of all examples, with brief descriptions. These examples should serve as a good starting point for writing your own code using cppdlr.

For the time being, not all use cases are covered by examples in the examples directory. However, the test directory of the repository contains tests of all the components of cppdlr, and these can also serve as useful examples (though they might not be as user-friendly as the examples in the examples directory). Therefore, in the list of other capabilities below, we list capabilities of cppdlr which are not currently covered by examples, and point to the relevant tests in the test directory which can serve as examples of these capabilities. This is a temporary measure, until we have a more comprehensive set of examples.

Example: form a DLR expansion via interpolation, and evaluate it in imaginary time and frequency

This example follows the example program in the file examples/dlr_interpolation.cpp. You should follow the code in that file as you read this example. If you see a definition you do not know, or need to look up a convention, you can find this information on the background page.

We first include the header file cppdlr.hpp, which is necessary to use cppdlr functionality, and use the cppdlr namespace. We then define an evaluator function, gfun, for an imaginary time Green’s function. In this case, we take a simple example: a Green’s function corresponding to a spectral function which is a discrete sum of delta functions:

\[\rho(\omega) = \sum_{i=1}^N A_i \delta(\omega - a_i).\]

In this case, we have taken each \(A_i\) to be a \(2 \times 2\) symmetric matrix. Using the Lehmann representation, defined on the background page, we see that this yields the following imaginary time Green’s function:

\[G(\tau) = \sum_{i=1}^N A_i K(\tau, a_i) \equiv \sum_{i=1}^N A_i \frac{e^{-\tau a_i}}{1+e^{-\beta a_i}}.\]

There is nothing special about this Green’s function, except that it is convenient for this example because it has a simple analytical form. We also define an evaluator for the Green’s function in fermionic Matsubara frequency space, which, by direct Fourier transform, is given by

\[G(i \nu_n) = \sum_{i=1}^N A_i K(i \nu_n, a_i) \equiv \sum_{i=1}^N \frac{A_i}{i \nu_n - a_i}.\]

Next we move to the main program. We first define the the inverse temperature \(\beta\), the number of orbital indices, which in this case is 2 since \(G\) is a \(2 \times 2\) matrix-valued function, the DLR cutoff parameter \(\Lambda\), and the desired accuracy \(\epsilon\) of our DLR expansion. We note that we took all the \(a_i\) above to be less than 1, so the spectral width \(\omega_{\max}\) of the Green’s function is less than 1; therefore, the DLR cutoff parameter \(\Lambda = \beta \omega_{\max}\) can be safely set to \(\beta\). If the spectral width is unknown, it is recommended to converge results with respect to \(\Lambda\). After this, we set the number of points at which we will test the accuracy of our DLR expansion, both in imaginary time and Matsubara frequency.

We now begin to see some of the basic functionality of cppdlr. We first obtain the DLR frequencies \(\omega_l\) by calling the function build_dlr_rf, supplying the DLR cutoff parameter and tolerance as input parameters. We obtain a vector of \(r = 31\) DLR frequencies, which are shown below for the given parameters. We note that although cppdlr works in non-dimensionalized variables (e.g., we consider \(\tau \in [0,1]\) rather than \(\tau \in [0,\beta]\)), we have converted back to the original physical variables in all figures on this page.

_images/dlr_rf.png

We next obtain an object of type imtime_ops. This class is responsible for all imaginary time operations on Green’s functions, such as interpolation, fitting, and convolution, and given a particular set of DLR frequencies, determined by \(\Lambda\) and \(\epsilon\), you only need one of these. The vector of DLR imaginary time grid nodes \(\tau_k\) can be extracted from this object using the get_itnodes method.

We next evaluate the Green’s function at the DLR imaginary time grid nodes by calling the evaluator function discussed above. In practice, you would supply your own Green’s function evaluator, which could involve a complicated program. Below, we plot the Green’s function, with the \(r = 31\) DLR imaginary time nodes indicated.

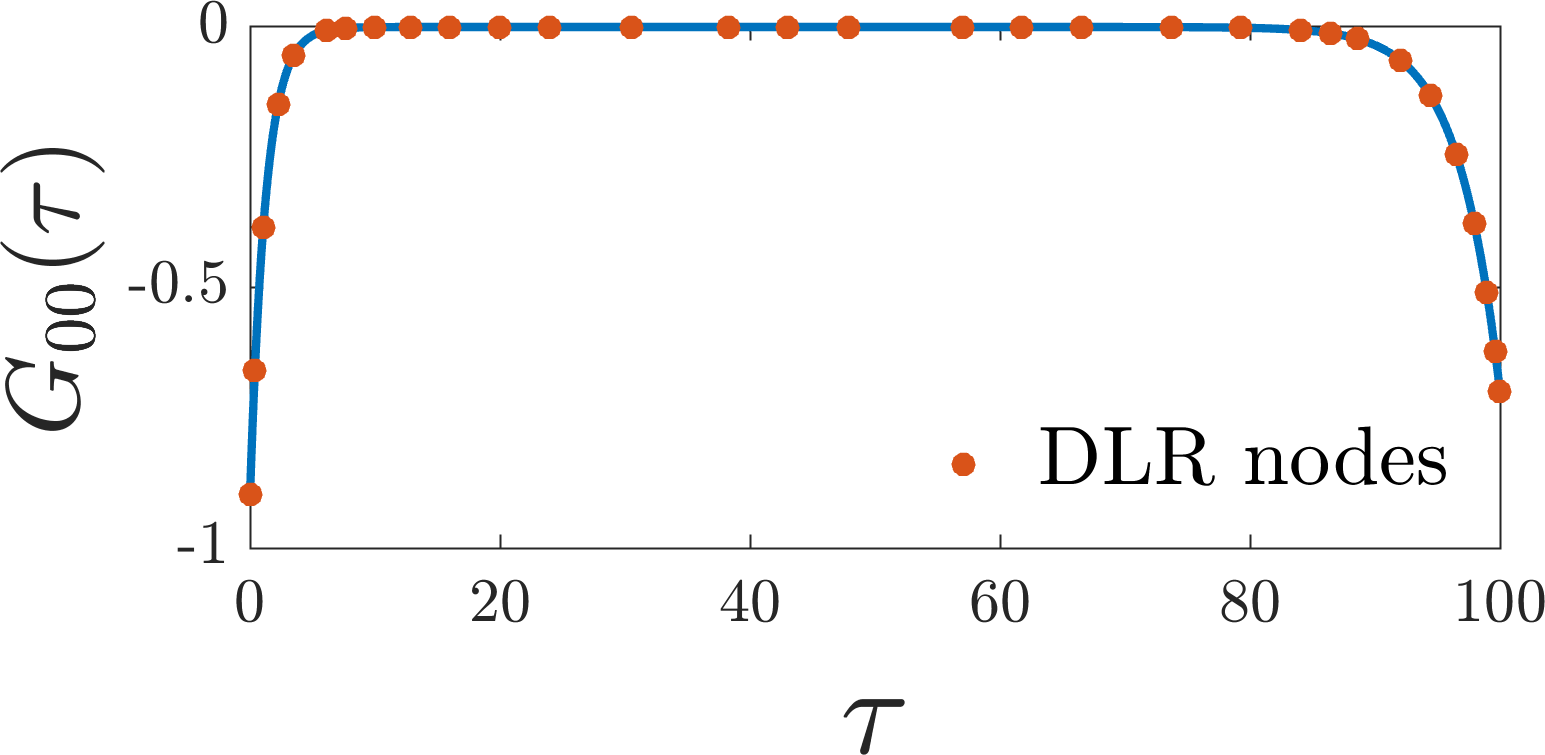
_images/gfun.png

Now that we have the values of the Green’s function on the DLR imaginary time grid, \(G(\tau_k)\), we can form its DLR expansion by obtaining its DLR coefficients \(\widehat{g}_l\) via the vals2coefs method of the imtime_ops object. We sometimes call this the interpolation step, since we are interpolating the Green’s function at the DLR nodes using an expansion in the DLR basis functions \(K(\tau, \omega_l)\). In other words, we solve the linear system

\[\sum_{l=1}^r K(\tau_k, \omega_l) \widehat{g}_l = G(\tau_k)\]

which constitutes an interpolation problem.

Having obtained the DLR expansion of \(G\) (characterized by its DLR coefficients \(\widehat{g}_l\)), we can now evaluate it at any imaginary time point \(\tau\) by simply evaluating the DLR expansion:

\[G(\tau) \approx \sum_{l=1}^r K(\tau, \omega_l) \widehat{g}_l.\]

This is done using the coefs2eval method of the imtime_ops object. Here, we evaluate the DLR expansion on an equispaced grid of \(\tau\) points generated by the function eqptsrel (this function generates the points in the relative time format used by cppdlr; please see the imaginary time point format section of the Background page for details). We also evaluate the true Green’s function, and compare the two. The pointwise error for the top-left entry of the Green’s function, \(G_00(\tau)\), is shown below.

_images/gfun_err_it.png

We see that the DLR expansion is correct to within the specified \(\epsilon = 10^{-10}\) tolerance.

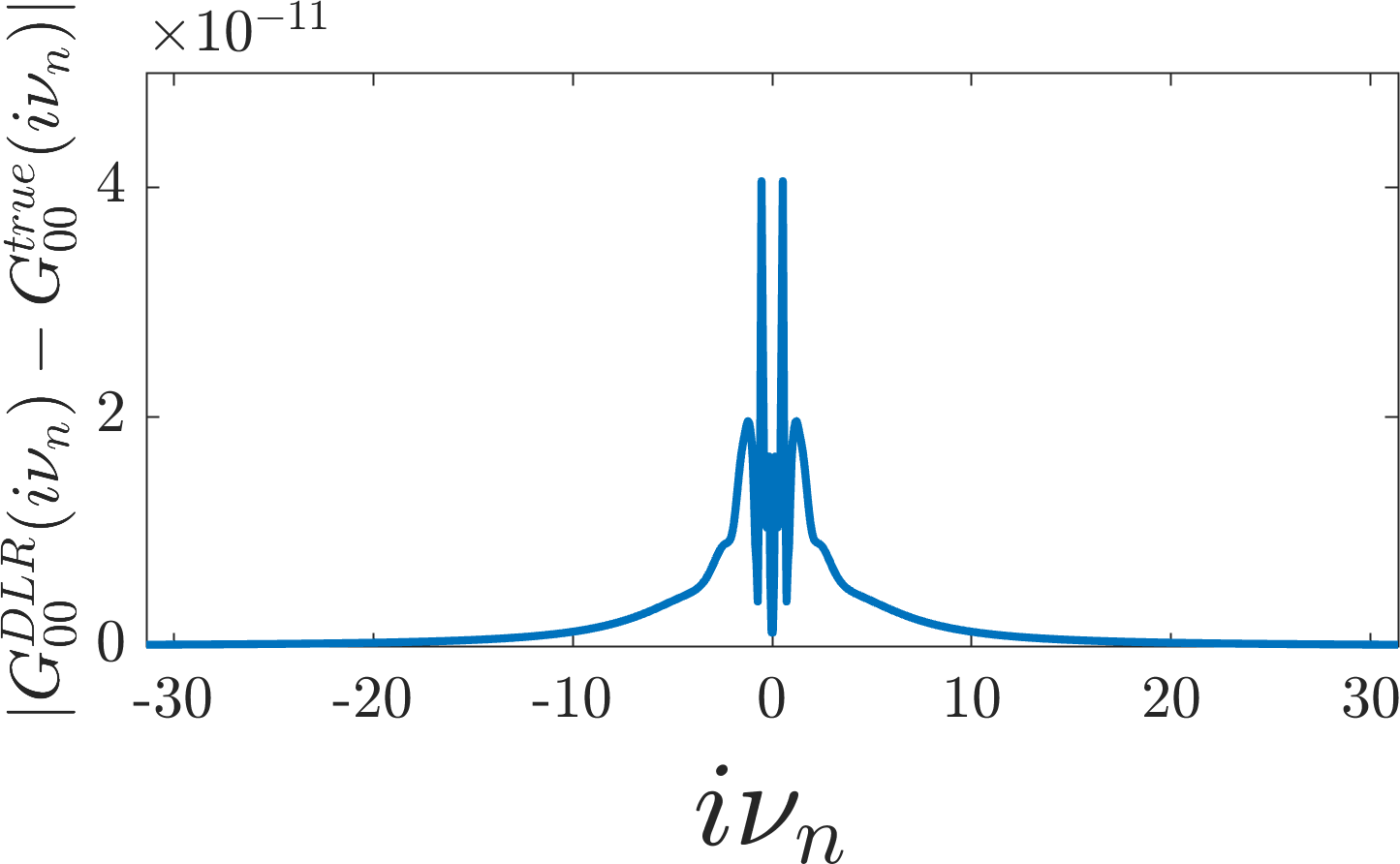
Since the Fourier transform of the DLR basis functions are known, we can directly evaluate the DLR expansion of \(G\) in the fermionic Matsubara frequency space:

\[G(i \nu_n) \approx \sum_{l=1}^r K(i \nu_n, \omega_l) \widehat{g}_l.\]

To do this, we first construct an object of type imfreq_ops. This class is analogous to the imtime_ops class, but is responsible for all Matsubara frequency operations. Here, we use its coefs2eval method to evaluate the DLR expansion of \(G\) at a large set of Matsubara frequencies, which in cppdlr are characterized by their index \(n\). Again comparing to the top-left entry \(G_00(i \nu_n)\) of the true Green’s function, we find agreement within the specified \(\epsilon = 10^{-10}\) tolerance.

_images/gfun_err_if.png

List of examples

The examples directory contains the following example programs, which are documented in detail in the files themselves.

  • examples/dlr_interpolation.cpp: form a DLR expansion via interpolation, and evaluate it in imaginary time and frequency. This example is described in detail above.

List of other cppdlr capabilities

For cppdlr use cases which are not covered by examples in the examples directory, relevant unit tests in the test directory can serve as useful examples. We list several such use cases below.

  • Obtain a DLR expansion by fitting to data in imaginary time: see the tests imtime_ops.fit_scalar, imtime_ops.fit_matrix, and imtime_ops.fit_matrix_cmplx in the file test/imtime_ops.cpp.
  • Compute the convolution of two DLR expansions: see the tests imtime_ops.convolve_scalar_real, imtime_ops.convolve_scalar_cmplx, imtime_ops.convolve_matrix_real, and imtime_ops.convolve_matrix_cmplx in the file test/imtime_ops.cpp.
  • Perform a “reflection” operation \(G(\tau) \mapsto G(\beta-\tau)\) on a Green’s function: see the test imtime_ops.refl_matrix in the file test/imtime_ops.cpp.
  • Compute the inner product of two DLR expansions: see the test imtime_ops.innerprod in the file test/imtime_ops.cpp.
  • Obtain a DLR expansion by interpolation on the DLR Matsubara frequency nodes: see the tests imfreq_ops.interp_scalar and imfreq_ops.interp_matrix in the file test/imfreq_ops.cpp.
  • Obtain symmetrized DLR grids, and obtain a DLR expansion by interpolation on these grids: see the tests imtime_ops.interp_matrix_sym_fer and imtime_ops.interp_matrix_sym_bos in the file test/imtime_ops.cpp for fermionic and bosonic Green’s functions, respectively, on a symmetric imaginary time grid. See the tests imfreq_ops.interp_matrix_sym_fer and imfreq_ops.interp_matrix_sym_bos in the file test/imfreq_ops.cpp for fermionic and bosonic Green’s functions, respectively, on a symmetric Matsubara frequency grid. All of these tests show how to obtain a symmetric set of DLR frequencies.
  • Given a fixed self-energy, solve the Dyson equation in imaginary time to obtain the Green’s function: see the tests dyson_it.dyson_vs_ed_real, dyson_it.dyson_vs_ed_cmplx, and dyson_it.dyson_bethe in the file test/dyson_it.cpp.
  • Solve the Dyson equation self-consistently in imaginary time, given an expression for the self-energy in terms of the Green’s function: see the test dyson_it.dyson_bethe_fpi in the file test/dyson_it.cpp.